Arduino + Matlab/Simulink: controlador PID
Uuno de nuestros más divertidos proyectos con Arduino! En este caso, empleando el sistema de comunicación serie, vamos a programar un controlador PID (un controlador que actúa proporcionalmente al valor del error, al de su derivada, y al de su integral) en Simulink, el programa de dibujar esquemas más caro de la historia.
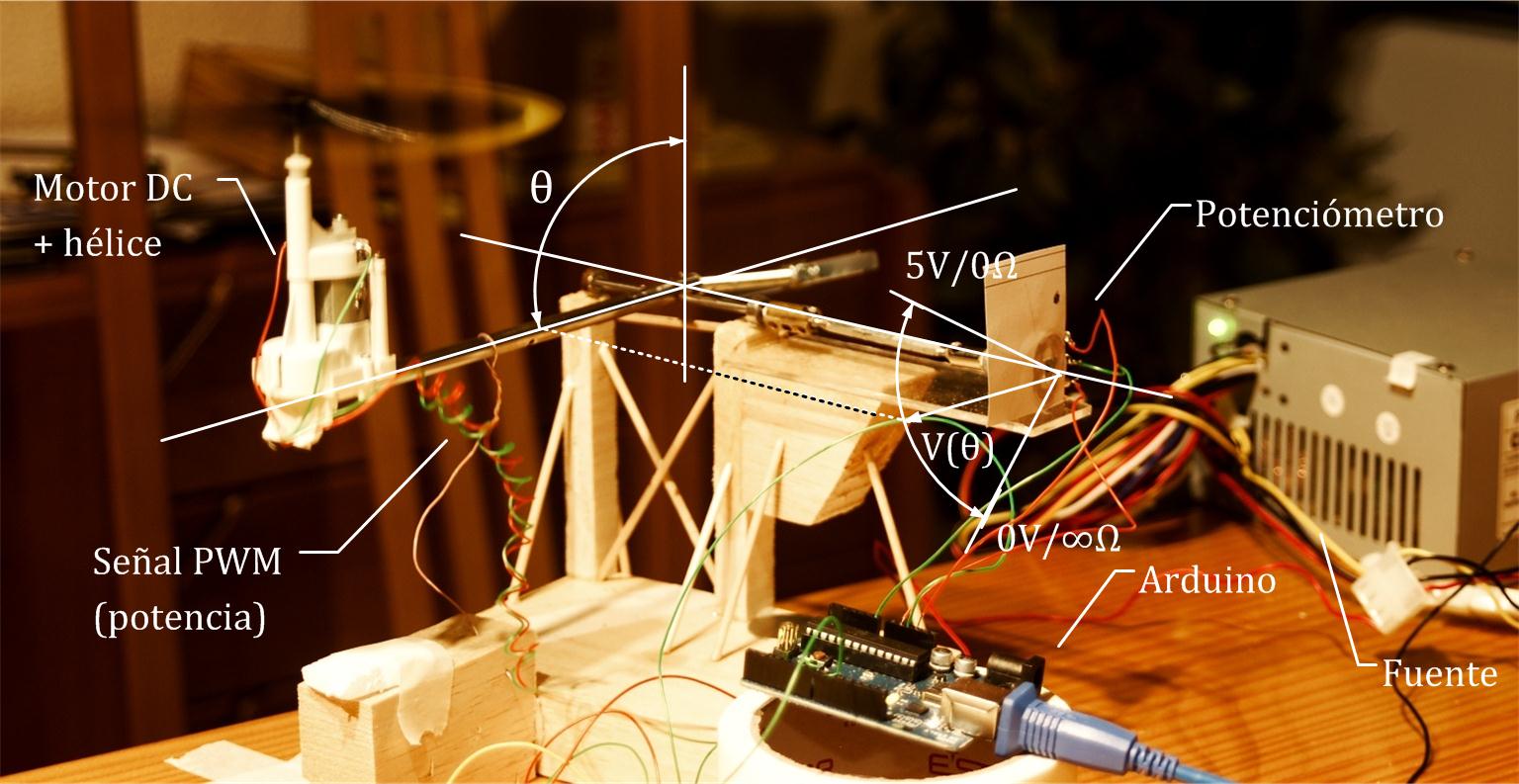
El objetivo es controlar la posición de un sistema muy simple (podría ser llamado “helicóptero de un grado de libertad” por alguien extremadamente idealista y “balancín a hélice” por alguien que lo fuera menos) y gradualmente ir complicado el sistema.
1. Introducción
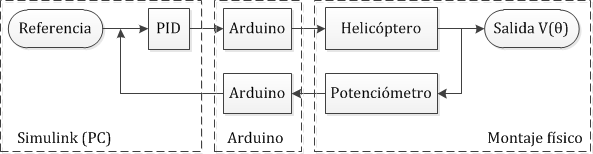
Como se observa, se trata de un brazo articulado con un motor en un extremo, unido a una hélice que proporciona más o menos sustentación en función del voltaje suministrado al motor. En la articulación del eje hay un potenciómetro solidario a él, que devuelve un voltaje \(V(\theta)\) entre 0V y 5V, en función del ángulo \(\theta\). El esquema del sistema de control es el siguiente:
De esta manera tenemos definida la variable de salida (posición del eje: voltaje transmitido por el potenciómetro) y la variable de control (sustentación de la hélice: voltaje proporcionado al motor). Nos falta pues un bucle de control (que programaremos en Simulink), una variable de entrada y una interfaz física.
2. Interfaz física
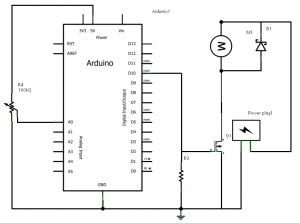
Tal y como se explica en una entrada anterior, el Arduino es incapaz por sí mismo de aportar el amperaje que necesita el motor, por lo que emplearemos un circuito de potencia consistente en un transistor MOSFET.
El microcontrolador enviará a la puerta del transistor una señal PWM, y por tanto esta misma señal PWM pero de potencia será la que reciba el motor. La representación de este montaje será la siguente:
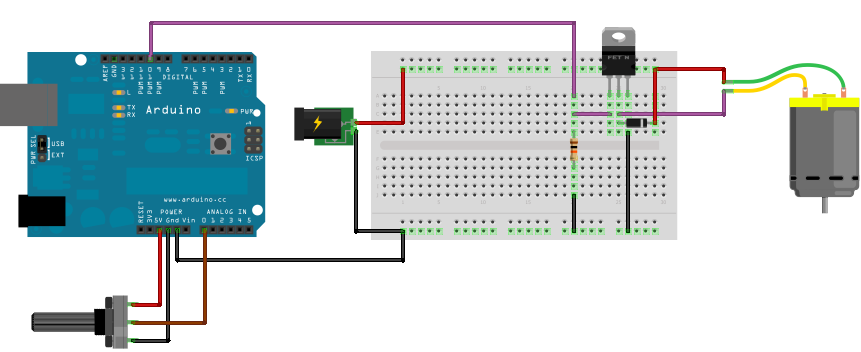
Esta es toda la parte física del problema: la planta que vamos a controlar, la variable de salida (ángulo del eje), la variable de control (potencia al motor) y el montaje que hemos realizado con el Arduino. A continuación la parte de código, tanto de Arduino como de Simulink/Matlab.
3. Programación
3.1. Arduino: interfaz I/O
En primer lugar, el código del Arduino debe ser capaz de (1) leer \(V(\theta)\) del potenciómetro, (2) enviarlo como dato a través del puerto serie, (3) recibir el dato de potencia necesaria al motor y (4) escribir dicho dato en la salida analógica como señal PWM. Hay que tener en cuenta que el conversor devuelve un valor entre 0 y 1024, que mapeamos a 0 y 255 para poder enviarlo como un solo bit unsigned.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int out = 0;
byte in = 0;
byte pinOut = 10;
void setup() {
// inicializar puerto serie
Serial.begin(9600);
// preparar output
pinMode(pinOut, OUTPUT);
}
void loop() {
// leer del pin A0 como
out = analogRead(A0);
// escalar para obtener formato uint8
out = map(out, 0, 1023, 0, 255);
// enviar en base 10 en ASCII
Serial.write(out);
// leer del serie si hay datos
if(Serial.available()){
in = Serial.read();
// escribir en el pin 10
analogWrite(pinOut, in);
}
// esperar para estabilizar el conversor
delay(20);
}
3.2. Simulink: bucle de control
Por otra parte, nuestro programa de Simulink debe recibir este dato de \(V(\theta)\) a través del puerto serie, compararlo con una referencia \(V_\text{ref}\) que controlaremos nosotros con un slider en la propia interfaz gráfica de Simulink, y, mediante un controlador PID, determinar la señal de control (potencia al motor) necesaria. Después debe enviarla a través del puerto serie en formato uint8, unsigned integer de 8 bits, que toma valores entre 0 y 255, ideales para la función analogWrite() de Arduino:
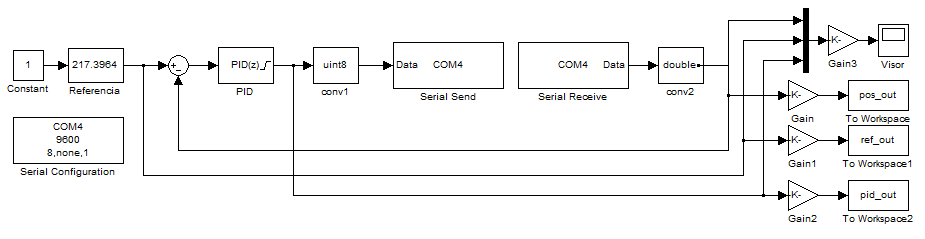
Dentro del bloque PID, se pueden editar los parámetros P, I y D, siendo los últimos que hemos empleado P = 0.26 , I = 0.9, D = 0.04 y una discretización de 10 ms. Otro dato a tener en cuenta es que la transmisión serie se hace en formato uint8, pero las operaciones se hacen en formato double, de ahí los conversores. Las ganancias K son de valor 5/1024 para pasar la señal a voltios reales.
Nota: este modelo de Simulink se puede descargar aquí.
A continuación, un vídeo de todo el sistema en funcionamiento (esta es una de las primeras pruebas, con otros parámetros del PID sin optimizar todavía):
Se puede observar cómo mediante el slider ajustamos la referencia (señal lila). El sistema, ajustando la señal de potencia entregada al motor (señal azul) va ajustando el ángulo \(\theta\) del eje hasta conseguir que el voltaje del potenciómetro \(V(\theta)\) (señal amarilla) coincida con la referencia que le hemos indicado. Incluso, a pesar de estar en una primera fase de pruebas, se observa que es capaz de resistir a Salva perturbaciones.
3.3. Matlab: postproceso de los datos recogidos
Si nos fijamos en el programa de Simulink anterior, se puede observar que no sólo se presentan en el visor las tres señales, sino que además se guardan en el espacio de trabajo de Matlab. Esto nos permite, a posteriori, procesar los resultados del proceso de control como queramos: identificación de sistemas, exportación a Excel… en este caso, nos contentamos con emplear la útil función externa savefigure() para obtener un gráfico vectorial PDF:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
%% Preparar la figura
f = figure('Name','Captura');
axis([0 length(ref_out) 0 5.1])
grid on
xlabel('Medida (-)')
ylabel('Voltaje (V)')
title('Captura de voltaje en tiempo real con Arduino')
hold all
%% Tratamiento
pos_out = pos_out(:);
pid_out = pid_out(:);
x = linspace(0,length(ref_out),length(ref_out));
%% Limpiar figura y dibujar
cla
plot(x,pid_out,'Color',[0.6,0.6,0.6],'LineWidth',2)
plot(x,ref_out,x,pos_out,'LineWidth',2)
legend('Control','Referencia','Posición','Location','Best');
%% Salvar el gráfico
savefigure('resultado','s',[4.5 3],'po','-dpdf')
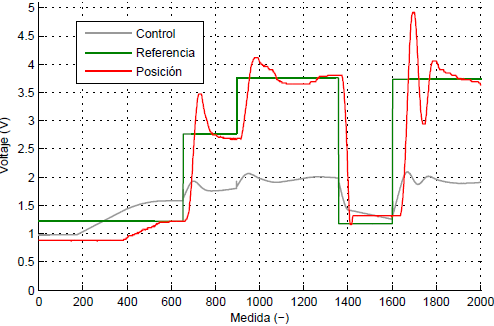
Ejecutando este código tras haber realizado otro ensayo del sistema, hemos obtenido el siguiente resultado:
Se observa en este caso que el motor requiere mucho menos voltaje (en gris) debido a que se trata de uno más potente que el inicial y que el sistema presenta todavía una sobreoscilación (overshoot) en la señal de salida (en rojo) cuando la señal de referencia (en verde) presenta una subida escalón, cosa que esperamos corregir en futuras versiones.
4. Conclusiones
En esta entrada se describe cómo es posible, con un presupuesto muy reducido, construir montajes que permiten poner en práctica la teoría del control PID. El siguiente desarrollo interesante sería realizar un control con dos grados de libertad en lugar de uno… not because it is easy, but because it is hard!
 Thanks for reading! To share this post, use this
permalink
Thanks for reading! To share this post, use this
permalink