Mathematica: Rosa de los Vientos
Uno de los principales problemas en ingeniería es la búsqueda y procesado de datos, a la hora de analizar o planificar cualquier cosa. Habitualmente esto implicaba visitas, peticiones, transcribir, y una infinidad de sinsabores, pero hoy en día las cosas han cambiado mucho. Un ejemplo típico en aeronáutica son las rosas de los vientos:

Se trata de recopilar datos históricos acerca de las direcciones en las que suele soplar el viento en un lugar en el que se pretende levantar un aeródromo para orientar la pista en la dirección preferente del viento, a fin de facilitar despegues y aterrizajes y evitar el viento cruzado.
Hoy en día sin embargo, existen herramientas que nos ayudan enormemente a realizar tareas pesadas como ésta. En concreto, vamos a ver como Mathematica nos hace la tarea mucho más llevadera.
Adquisición y proceso de datos
En primer lugar, vamos a obtener los datos de viento de una estación metereológica en concreto a través del servidor de datos de Wolfram Research. En concreto, usaremos como ejemplo el aeropuerto de Valencia, de código LEVC, desde el 1/11/2008 al 1/11/2009:
1
2
3
sitio = "LEVC";
data = Last /@ WeatherData[sitio, "WindDirection",
{{2008, 11, 1}, {2009, 11, 1}}];
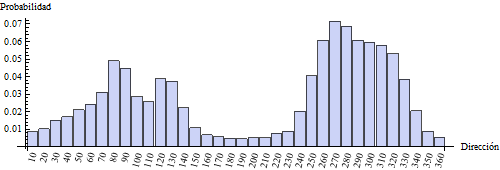
A continuación realizamos un histograma de los datos, dejando al programa elegir el método de espaciado oportuno (habitualmente Scott o Sturges para sets pequeños, Freedman – Diaconis para los más grandes):
1
2
data2 = HistogramList[data, Automatic, "Probability"][[2]];
data2dir = HistogramList[data, Automatic, "Probability"][[1]];
Representación de los datos
Podemos a continuación representar dicho histograma de la forma habitual:
1
2
3
4
5
g0=BarChart[data2,
ImageSize->500,
AspectRatio->0.3,
AxesLabel->{"Dirección","Probabilidad"},
ChartLabels->Placed[data2dir,Below,Rotate[#,Pi/2.4]&]]
Con lo que obtenemos el siguiente gráfico:
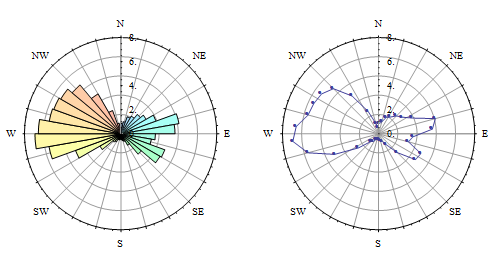
Estos mismos datos se pueden poner en forma de gráfico polar, tanto de columnas como de puntitos, a gusto del consumidor. La segunda forma, por alguna razón, suele ser la más habitual en la literatura española.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
g11 = SectorChart[{Table[{1, 100 i}, {i, data2}]},
SectorOrigin -> {Pi/2, "Clockwise"}, PolarAxes -> True,
PolarGridLines -> Automatic, PolarTicks -> {"Direction", Automatic},
ChartBaseStyle -> Directive[Opacity[1], EdgeForm[Thin]]]
g12 = ListPolarPlot[
Table[{(2 \[Pi])/Length[data2] (1 - i) + \[Pi]/2 - \[Pi]/
Length[data2], 100 data2[[i]]}, {i, 1, Length[data2]}],
PolarAxes -> True, PolarGridLines -> Automatic,
PolarTicks -> {"Direction", Automatic}, Joined -> True,
PlotStyle -> Thickness[0.005], Mesh -> All,
PlotMarkers -> {Automatic, 5}, ImageSize -> Small]
GraphicsRow[{g11, g12}, ImageSize -> 500]
Las dos opciones quedan pues de la siguiente manera, ya con los datos representados de forma polar según la probabilidad porcentual de la dirección del viento:
Comparación con aeropuertos reales
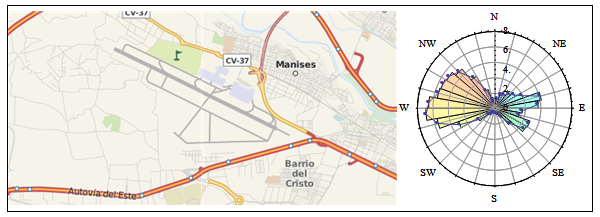
Para comparar esta orientación ideal puede ser muy útil obtener imágenes de los aeropuertos reales. La opción más sencilla es usar una base de datos de mapas gratuitos a la que se puede acceder programáticamente conociendo la latitud, la longitud y el nivel de zoom y transformando estos datos en dos parámetros \(x\) e \(y\) con los que el servidor nos envía los cuadraditos:
%%% x=\left\lfloor\frac{long+180}{360}2^{zoom}\right\rfloor %%% %%% y=\left\lfloor\left(1-\frac{\ln\left(\tan\left( lat/180\cdot \pi\right)+\frac{1}{\cos(lat/180\cdot \pi)}\right)}{\pi}\right)2^{zoom-1}\right\rfloor %%%
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
zooml = 13;
Deg2Num[lat_, lon_,
zoom_] := {IntegerPart[(2^(-3 + zoom)*(180 + lon))/45],
IntegerPart[
2^(-1 + zoom)*(1 - Log[Sec[Degree*lat] + Tan[Degree*lat]]/Pi)]}
{x, y} = Deg2Num[WeatherData[sitio, "Latitude"],
WeatherData[sitio, "Longitude"], zooml];
g1 = Show[g11, g12, ImageSize -> Small];
g2 = GraphicsRow[{Import[
"http://otile2.mqcdn.com/tiles/1.0.0/osm/" -> ToString[zooml] ->
"/" -> ToString[x - 1] -> "/" -> ToString[y] -> ".png"],
Import[
"http://otile2.mqcdn.com/tiles/1.0.0/osm/" -> ToString[zooml] ->
"/" -> ToString[x] -> "/" -> ToString[y] -> ".png"], g1},
Spacings -> 0, ImageSize -> 600, Frame -> True]
Con lo que ya podemos obtener una imagen comparativa de ambos resultados:
Conclusiones
Como hemos visto, resulta (relativamente) sencillo crear un programa que dado cualquier aeropuerto o estación metereológica nos grafique su rosa de los vientos y un mapa local; lo importante de esto es que se puede adaptar a cualquiera de los millones de todo tipo de datos (metereológicos, demográficos, económicos, biológicos, termoquímicos, etc.) que Wolfram Research pone a tu disposición (después de pagar su licencia, claro está). No más Excel!
 Thanks for reading! To share this post, use this
permalink
Thanks for reading! To share this post, use this
permalink