Mathematica y la Solución de Navier
En esta entrada se presenta uno de los problemas a los que nos enfrentamos habitualmente los ingenieros. Se trata de combinar una solución analítica clásica (propuesta en el siglo XIX por el físico e ingeniero francés Claude Navier) a un problema habitual en cualquier campo, empleando las herramientas informáticas del siglo XXI.
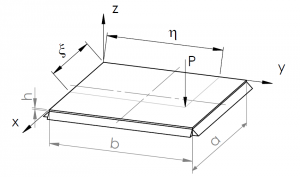
Plantearemos cómo se hace el desarrollo teórico y cómo las expresiones resultantes se pueden programar en Mathematica, para después usar dichas ecuaciones en gráficas y programas concretos. En este caso, se trata de averiguar qué pasa cuando sometemos una placa plana como la de la derecha a una carga puntual.
1. Planteamiento teórico
En primer lugar, vamos a ver cuál es el desarrollo teórico del problema, demostrando al mismo tiempo cómo programar las ecuaciones en Mathematica. Intuitivamente, cuando sometemos una placa a una carga esta se deformará. Vamos a calcular en primer lugar estas deformaciones.
1.1. Deformaciones
Comenzamos por plantear la ecuación clásica de una placa de Kirchhoff de dimensiones \(a \times b \times h\), módulo de Young \(E\) y módulo de Poisson \(\nu\) que sufre una carga \(q = q(x,y)\):
%%% \nabla ^4w = -\frac{q}{D}\equiv \frac{ \partial ^4w}{\partial x^4}+2\frac{ \partial ^4w}{\partial x^2\partial y^2}+\frac{ \partial ^4w}{\partial y^4}=-\frac{q}{D},\qquad D:= \frac{ h^3E}{12\left(1-\nu ^2\right)} %%%
Suponemos que la carga sigue una distribución senoidal del tipo:
%%% q=q(x,y)=q_0\sin \left(\frac{n \pi x}{a}\right)\sin \left(\frac{m \pi y}{b}\right) %%%
Y que la solución se puede representar mediante una función de prueba como la siguiente:
%%% w=C \sin \left(\frac{n \pi x}{a}\right)\sin \left(\frac{m \pi y}{b}\right) %%%
Empleando las condiciones de contorno de la restricción simple (el desplazamiento en los bordes es nulo, así como el momento de reacción):
%%% (1)\quad w(0) = w(a)=0, %%% %%% (2)\quad M_{\text{xx}}(0) = w_{\text{xx}}(0)=M_{\text{xx}}(a)=w_{\text{xx}}(a)=0, %%% %%% (3)\quad w(0) = w(b)=0, %%% %%% (4)\quad M_{\text{yy}}(0) =w_{\text{yy}}(0)=M_{\text{yy}}(b)=w_{\text{yy}}(b)=0 %%%
Podemos obtener la siguiente solución general para la deformación en \(z\):
%%% w=w(x,y)=\frac{q_0}{\pi ^4D}\frac{\sin \left(\frac{n \pi x}{a}\right)\sin \left(\frac{m \pi y}{b}\right)}{\left(\frac{n^2}{a^2}+\frac{m^2}{b^2}\right)^2} %%%
Que procedemos a programar en Mathematica:
1
2
3
wnm = (1/(Pi^4*Dv))*(pnm/((n/a)^2 + (m/b)^2)^2)
*Sin[(n*Pi*x)/a]*Sin[(m*Pi*y)/b];
Dv = (Ev*h^3)/(12*(1 - Nu^2));
En el caso que nos ocupa, una carga de valor \(P\) concentrada en un solo punto que tiene coordenadas arbitrarias (\(\xi\),\(\eta\)), podemos usar la función delta de Dirac para escribir:
%%% q=q(x,y)=P \delta (x-\xi ,y-\eta ) %%%
Que se introduce en el programa de la siguiente manera:
1
p[x_, y_] := P DiracDelta[x - Xi, y - Eta];
Es aquí donde hacemos uso de la solución propuesta por Navier, que consiste en representar una carga general como un desarrollo en serie de Fourier:
%%% P \delta (x-\xi ,y-\eta )=\sum_{n=1}^{\infty } \sum_{m=1}^{\infty} p_{\text{nm}}\sin \left(\frac{n \pi x}{a}\right)\sin \left(\frac{m \pi y}{b}\right) %%%
Empleando ahora las propiedades de ortogonalidad de los términos de Fourier, podemos concluir que los términos de la serie serán:
%%% p_{\text{nm}}=\frac{4}{a b}\int_0^a\int _0^bP \delta (x-\xi ,y-\eta )\sin \left(\frac{n \pi x}{a}\right)\sin \left(\frac{m \pi y}{b}\right)dydx= %%%
%%% =\frac{4P}{a b}\sin \left(\frac{n \pi \xi }{a}\right)\sin \left(\frac{m \pi \eta }{b}\right) %%%
Aunque podemos dejar que Mathematica se encargue:
1
2
pnm = (4/(a*b))*Integrate[p[x, y]*Sin[(n*Pi*x)/a]*Sin[(m*Pi*y)/b]
,{x, 0, a}, {y, 0, b}];
Introduciendo estos términos en la solución general hallada anteriormente y aplicando el principio de superposición, podemos hallar la solución para nuestra carga singular:
%%% w(x,y,\xi ,\eta )=P K(x,y,\xi ,\eta )= %%%
%%% =\frac{4P}{\pi ^4a b D}\sum _{n=1}^{\infty } \sum _{m=1}^{\infty } \frac{\sin \left(\frac{n \pi x}{a}\right)\sin \left(\frac{m \pi y}{b}\right)\sin \left(\frac{n \pi \xi }{a}\right)\sin \left(\frac{m \pi \eta }{b}\right)}{\left(\frac{n^2}{a^2}+\frac{m^2}{b^2}\right)^2} %%%
Que registramos truncando el desarrollo hasta un número variable de términos, cuyo máximo ajustaremos a la hora del cálculo:
1
w = Sum[wnm, {n, 1, nmax}, {m, 1, mmax}];
Se observa que es útil, de cara a posibles generalizaciones, definir una función \(K\) que representa la deformación debido a una carga singular de valor unitario:
%%% K(x,y,\xi ,\eta )= \sum _{n=1}^{\infty } \sum _{m=1}^{\infty } \frac{4}{\pi ^4a b D}\frac{\sin \left(\frac{n \pi x}{a}\right)\sin \left(\frac{m \pi y}{b}\right)\sin \left(\frac{n \pi \xi }{a}\right)\sin \left(\frac{m \pi \eta }{b}\right)}{\left(\frac{n^2}{a^2}+\frac{m^2}{b^2}\right)^2} %%%
1.2. Tensiones
Estas deformaciones causan tensiones en la placa, pudiendo incluso llegar a romperla. El objetivo habitual de este tipo de cálculos es averiguar si la placa aguantará la tensión. En primer lugar, para realizar el cálculo de tensiones, necesitaremos que Mathematica calcule las derivadas de la solución encontrada anteriormente:
1
2
3
wxx = D[w, x, x];
wyy = D[w, y, y];
wxy = D[w, x, y];
De la teoría clásica de las placas de tipo Kirchhoff, tenemos que:
%%% \sigma_{xx}=\frac{12h/2}{h^3}M_{\text{xx}}=-D\frac{12h/2}{h^3}\left(w_{\text{xx}}+\nu w_{\text{yy}}\right) %%% %%% \sigma_{yy}=\frac{12h/2}{h^3}M_{\text{yy}}=-D\frac{12h/2}{h^3}\left(w_{\text{yy}}+\nu w_{\text{xx}}\right) %%% %%% \tau_{\text{xy}}=-D \frac{6\left(1-\nu ^2\right)}{h^2(1+\nu )}w_{\text{xy}} %%%
Lo que expresamos de la siguiente manera:
1
2
3
Sigmaxx = (-((Ev*(h/2))/(1 - Nu^2)))*(wxx + Nu*wyy);
Sigmayy = (-((Ev*(h/2))/(1 - Nu^2)))*(wyy + Nu*wxx);
Tauxy = (-((Ev*(h/2))/(1 + Nu)))*wxy;
A continuación y dado que suponemos tensión plana, dentro de las hipótesis del modelo de Kirchhoff, podemos calcular las tensiones principales:
%%% \left(\sigma _1 \ \sigma _2 \right)=\frac{\sigma _x+\sigma _y}{2}\pm \sqrt{\left(\frac{\sigma _x-\sigma _y}{2}\right)^2+\tau _{\text{xy}}{}^2} %%%
Que programadas quedan como:
1
2
Sigma1 = (Sigmaxx + Sigmayy)/2 + Sqrt[((Sigmaxx - Sigmayy)/2)^2 + Tauxy^2]
Sigma2 = (Sigmaxx + Sigmayy)/2 - Sqrt[((Sigmaxx - Sigmayy)/2)^2 + Tauxy^2]
Ahora podemos calcular una tensión equivalente, por ejemplo la planteada por von Mises a principios del s. XX:
%%% \sigma _{e (\text{VM})}=\sqrt{\sigma _1{}^2-\sigma _1\sigma _2+\sigma _2{}^2} %%%
Para finalmente programarla de la siguiente manera:
1
Sigmae = Sqrt[Sigma1^2 - Sigma1*Sigma2 + Sigma2^2];
2. Caso de ejemplo
2.1. Gráficas
Una vez obtenidas y programadas las bases teóricas, ya podemos realizar cálculos de casos concretos. Una de las aplicaciones prácticas más clásicas es la obtención de gráficas con la distribución de los campos de tensiones. Por ejemplo, suponiendo los siguientes datos de ejemplo, todos en SI:
%%% \text{E}= 150\ 10^9,\ h= 0.001,\ \nu = 0.3,\ a= 1,\ b= 1,\ P= -100 %%%
1
datos = {Ev = 150*10^9, h = 0.001, Nu = 0.3, a = 1, b = -100}
Y un desarrollo polinómico de orden 4 (de tal manera que limitemos razonablemente la expansión de Fourier), haciendo:
1
2
nmax = 4;
mmax = 4;
Podemos calcular y representar las distribuciones de tensión/deformación de distintas formas. Para ello vamos a suponer dos casos en los que la carga se sitúa en posiciones distintas:
%%% \begin{array}{c} \text{Carga en el centro }&=(\xi = 0.5,\eta =0.5)\\ \text{Carga en la esquina }&=(\xi = 0.9,\eta = 0.9) \end{array} %%%
1
2
carga1 = {Xi -> 0.5, Eta -> 0.5};
carga2 = {Xi -> 0.9, Eta -> 0.9};
2.1.1. Representación de los campos por separado
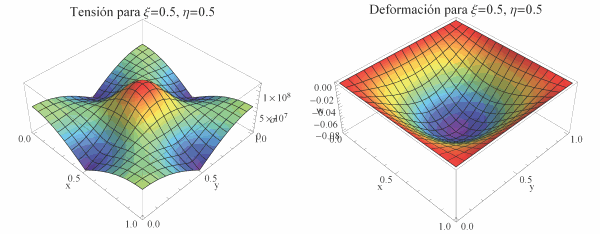
Una primera opción es representar en ambos casos las tensiones y las deformaciones en gráficas separadas. Para el caso de carga centrada en la placa, vemos cómo se deforma más por el centro y cómo es ahí donde se concentran las tensiones:
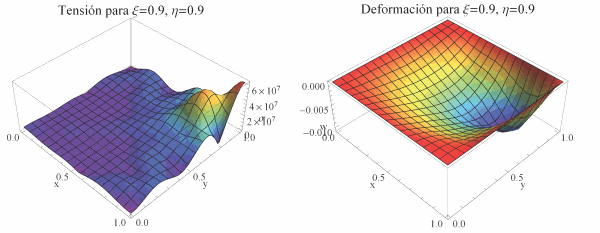
Para el segundo caso, vemos como la carga en una esquina causa una deformación en ese lugar, pero la placa sufre menos tensiones, ya que parte de ellas pasan a los soportes, que están más cerca:
El código empleado para representar estas figuras es el siguiente, repitiendo el mismo patrón para el resto de gráficos:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(* Soluciones numéricas *)
SigmaeM1 = Sigmae /. datos /. carga1;
wM1 = w /. datos /. carga1;
SigmaeM2 = Sigmae /. datos /. carga2;
wM2 = w /. datos /. carga2;
(* Ejemplo de gráfico para la primera solución *)
Plot3D[SigmaeM1, {x, 0, 1}, {y, 0, 1},
ColorFunction -> "Rainbow",
PlotRange -> Full,
ViewPoint -> {2, -2, 2.4},
AxesLabel -> {"x", "y", "Sigma"},
PlotLabel -> "Tensión para Xi=0.5, Eta=0.5"
]
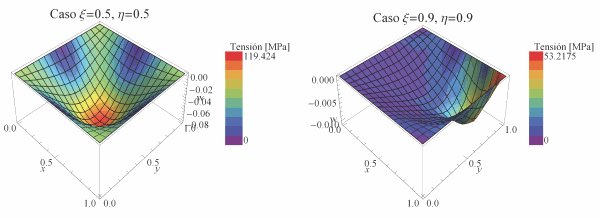
2.1.2. Representación conjunta de deformación y tensión
Otra opción interesante es la de representar la tensión en forma de color en el gráfico de deformaciones, lo cual es una manera habitual en programas comerciales de representarla:
2.2. Interfaz gráfica manipulable
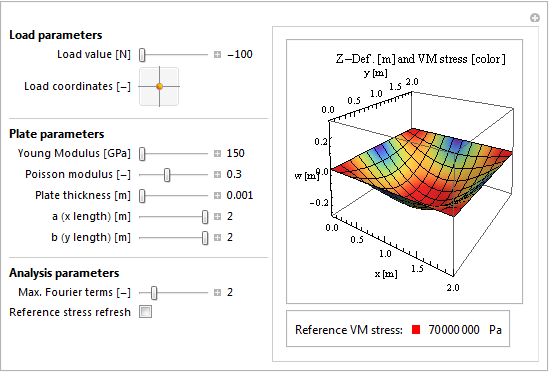
Otra opción que aprovecha la gran capacidad de programación de Mathematica es la de programar una interfaz que nos permita manipular en tiempo real todos los parámetros del problema y obtener la visualización inmediatamente. Aquí una captura de pantalla, más abajo se puede descargar el código para usarla o bien hacerlo directamente en la web de Wolfram donde está colgada.
3. Conclusiones
Creo que es interesante observar cómo el software matemático simbólico actual puede dar un nuevo sentido a soluciones y técnicas matemáticas analíticas de otros siglos, de tal manera que se puedan utilizar con sencillez en la resolución de problemas de ingeniería actuales. Esta solución analítica se podría emplear, por ejemplo, para validar códigos de resolución numérica mediante el Método de los Elementos Finitos, obtener representaciones exactas, o realizar rápidamente prediseños.
 Thanks for reading! To share this post, use this
permalink
Thanks for reading! To share this post, use this
permalink